温度对GH4169镍基高温合金形变过程位错演化的影响

传统的试验方法研究材料的宏观形变行为已非常成熟,但采用该方法存在试验周期长、成本高等不足,并且无法直接观测材料内部的微观形变及力学行为。因此,为了降低材料特性研究时对试验的过分依赖,可描述多晶相互作用的晶体塑性理论及分子动力学理论得以发展。并且,近年来计算机性能的提升也加速了基于晶体塑性理论或分子动力学理论的金属材料形变特性的研究进程。但是,晶体塑性有限元理论多用于模拟晶粒级细观尺度下的形变行为,无法体现材料在形变过程中的原子构型及位错的演化,而用于描述原子在外力作用下最基本运动细节的分子动力学模拟则可以弥补这一短板。分子动力学模拟需依据材料经验力场及原子初始位置计算其势能,通过求导的方法分析体系内各个原子的受力情况,进而基于牛顿运动方程,在极短的时间间隔(1×10-15s)内计算原子新的位置及受力,如此反复直至计算收敛[1-2]。因此,分子动力学模拟可以实时捕捉体系的动态形变,为在原子尺度上研究微观形变机制奠定了基础。ChenB等[3]建立了具有多种取向位错网的单晶镍基高温合金的分子动力学模型,通过对比体系能量及位错网演化过程,为建立更加精确的界面位错网模型提供依据。之后,LiNL和WuWP等[4]对引入界面位错网的分子动力学模型施加单轴拉伸载荷及循环载荷,通过分析材料形变过程中的位错演化、层错/滑移运动及应力-应变行为,评估应变率、温度对材料力学行为及循环形变机制的影响。LiXT等[5]揭示了位错发射与孔洞和缺陷的相互作用机理,认为位错发射会导致裂纹尖端钝化,是裂纹尖端脆性扩展演化为韧性扩展的主要因素。祝占伟[6]采用分子动力学模拟分析了镍基合金中五重孪晶的形成机制及形变机理。本文建立了LAMMPS分子动力学仿真原子结构模型,进行了室温(300K)与高温(600和920K)条件下的单轴拉伸仿真,讨论了温度对模型内部位错演化及力学行为的影响。

1、分子动力学模型

1.1　相互作用势函数

本文采用嵌入原子法(Embedded-AtomMethod,EAM)势函数[7]来描述原子间作用力的相互作用,EAM势是一种描述金属键最常用、最精确的相互作用模型,并且常用于描述原子尺度下的扩散、变形、熔化和烧结等过程[8-10]。EAM势中总能量Etot的计算公式如下,其中,系数1/2是为了避免一对相互作用的重复计算。

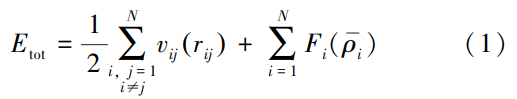
式中:vij(rij)为分离距离为rij的原子i与原子j之间的一对相互作用能;Fi为原子i的嵌入能,可以描述为局部电子密度ρi的函数;N为体系内共参与计算的原子对的数量。ρi的表达式为:

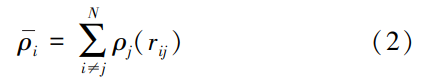
式中:ρj(rij)为将原子i赋值到分离距离为rij的原子j的电子密度函数。采用用于表示接近等原子成分组成下的Fe-NiCr-Co-Al的高度理想化面心立方FCC混合物的EAM势函数[7],该EAM势旨在模拟复杂系统的性质,可以较为精确地模拟系统中各类原子之间的相互作用。

1.2　原子结构模型

GH4169镍基高温合金粉末中存在超过10种元素,而Ni、Cr、Al与Fe元素的占比超过了元素总体含量的90%(质量百分数)。因此,为了在简化原子结构模型建模的同时,尽可能地保证多体相互作用的准确性,建立GH4169镍基高温合金原子结构模型时仅考虑Ni、Cr、Al与Fe共4种主要元素[9],4种元素的含量分别为52%、10%、1%与37%,即Ni52Fe37Cr10Al1。由于GH4169镍基高温合金中Ni元素含量最多,因此,在后续建模过程中,首先,依据镍基合金晶体类型建立适当尺寸的面心立方结构Ni单晶晶格模型。然后,依据Cr、Al与Fe这3种元素占比,分别在Ni单晶晶格模型中的FCC格位上随机替换Ni原子,形成一种高度类似于GH4169镍基高温合金元素组成的Ni52Fe37Cr10Al1原子结构,用于后续分子动力学计算。需要说明的是,Ni元素的点阵常数aNi=3.52Å作为常数用于后续建模。计算原子尺度下的GH4169镍基高温合金单轴拉伸应力-应变关系时,首先,建立尺寸(无量纲)为40×40×40的面心立方结构Ni单晶晶格模型,结合Ni元素的点阵常数可知,该晶格模型在x、y与z方向上的实际尺寸分别为40aNi、40aNi与40aNi。最终模型包含的原子总数为256000个,其中Ni原子有133120个、Fe原子有94720个、Cr原子有25600个、Al原子有2560个,最终模型如图1所示。

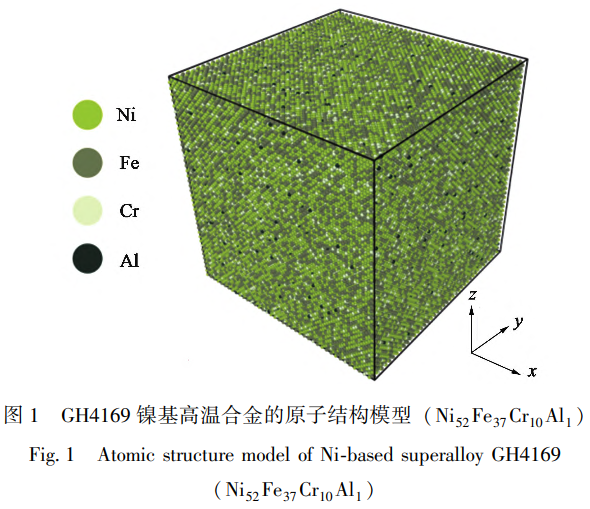
施加单轴拉伸载荷之前,首先在NVE(原子数-体积能量,Number-Volume-Energy)系综(恒定原子序数,恒温,不恒压)下对模型弛豫50ps,保证系统处于平衡状态。然后,利用Nose-Hoover热浴法设置环境温度,并且通过NVT(原子数-体积-温度,Number-Volume-Temperature)系综用应变控制对原子结构模型施加单轴拉伸载荷,应变率为1×109s^-1。计算过程中每间隔5ps输出环境热力学信息,以监控仿真是否平稳运行。通过设置变量的方法计算不同时刻体系的应力与应变数值,以绘制应力-应变曲线。仿真过程时间步长为0.001ps,每隔5ps输出体系形变结果。此外,通过改变环境温度(300、600和920K),以探究温度对GH4169镍基高温合金应力应变关系的影响。需要说明的是,整体计算过程包含minimize过程、弛豫过程、fix-deform过程,拉伸载荷加载过程中以载荷施加完毕为形变过程结束时刻,因此,并未关注整体计算时间。5000个时间步长是为了降低计算结果文件体积的同时保证输出计算结果可以精确反应整体形变过程。

2、结果与讨论

2.1　不同温度下的微观应力-应变关系

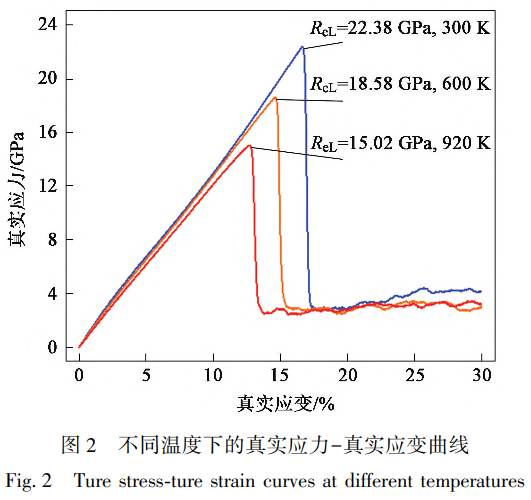
为了探究原子级纳米尺度下温度对GH4169镍基高温合金单轴拉伸力学性能及形变机制的影响,在300、600和920K条件下对原子结构施加单轴拉伸载荷,计算得到的真实应力-真实应变曲线,如图2所示。研究表明,分子动力学模拟过程中应变率的大小对材料弹性行为的影响可以忽略,更高的应变率仅表现出更高的屈服强度与更差的塑性[4]。从图2中可以看,不同温度下的真实应力-真实应变曲线均可划分为3个区域,即随着应变的增加,依次为应力线性增加的弹性区、应力骤降的塑性激活区与应力稳定的应力释放区[11]。与宏观应力-应变曲线不同的是,微观尺度下的应力-应变曲线在进入塑性激活区后应力变化呈现先骤降后波动的特征,这是因为在进入屈服阶段后原子结构内部会形成大量位错,随着应变的增加,位错会增殖与运动,因此,位错与位错之间、位错与其他晶体学结构之间会出现相互作用,这些相互作用一定程度上会使位错塞积,甚至消失,最终导致应力波动。应力骤降是由于Shockley位错发生反应,演化为其他类型位错或泯灭,此时体系内应力释放,导致应力下降。此外,随着温度的升高,GH4169镍基高温合金的屈服强度ReL逐渐下降,分别为22.38、18.58和15.02GPa。同样地,屈服应变也随温度的升高而降低,分别为16.65%、14.63%和12.67%,这表明温度越高,纳米原子GH4169镍基高温合金结构越容易形成位错,导致塑性形变。利用不同温度下弹性区的真实应力-真实应变曲线拟合得到的弹性模量分别为125.9、125.3和119.1GPa,可以看出,当温度低于920K时,材料的弹性模量十分接近,而当温度达到920K时,弹性模量下降了6.8GPa,这从纳米尺度上证明了GH4169镍基高温合金具有良好的920K高温抗性。

2.2　形变过程中原子构型演化

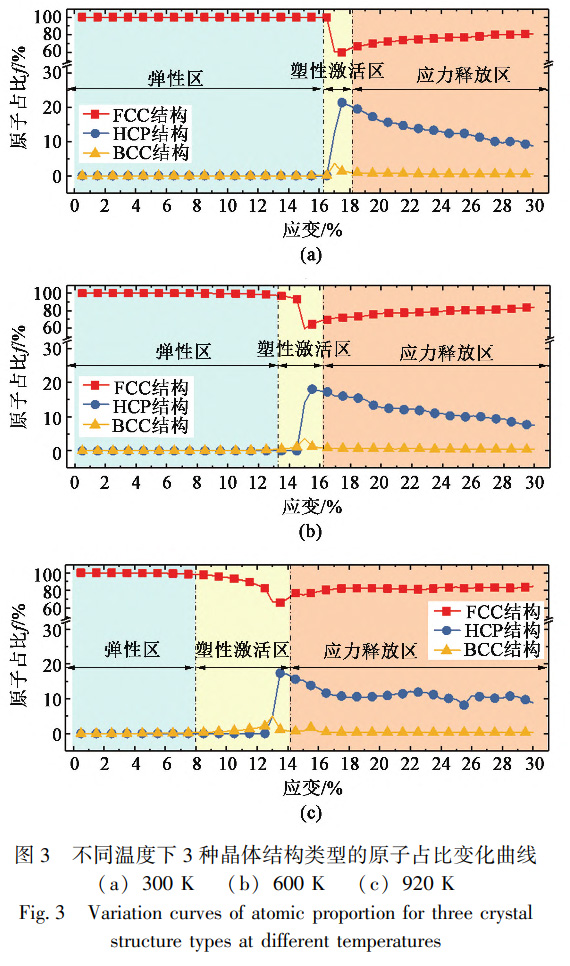
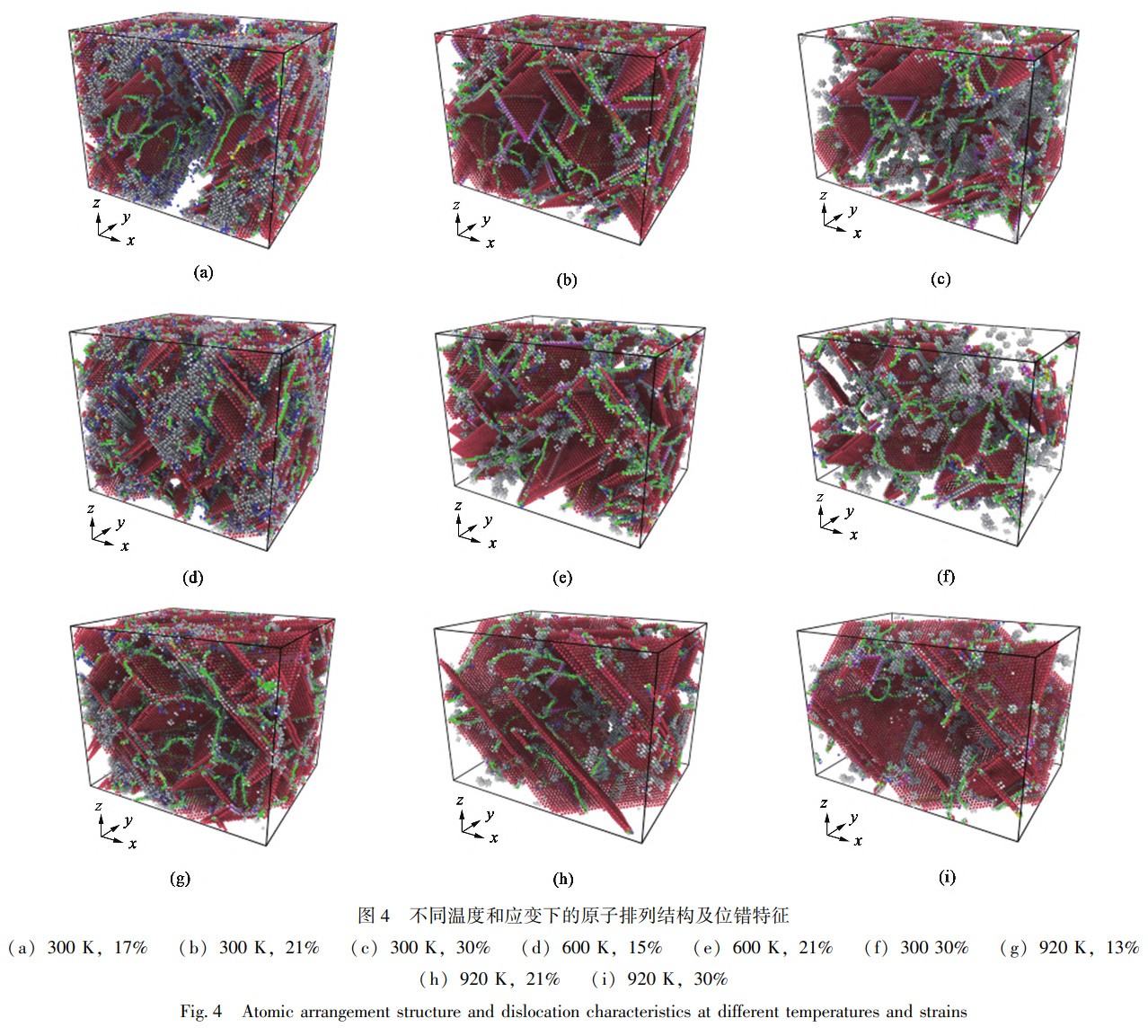
图3为不同温度下随应变增加原子结构模型中3种不同晶体结构类型的原子占比变化情况。从图3中可以看出,形变初期3种晶体结构所含原子数保持稳定,且均为面心立方FCC结构,这与弹性阶段对应。随着应变的增加,面心立方FCC结构原子占比降低,与此同时,体心立方BCC与六方密排HCP结构原子占比增多,此时对应应力-应变曲线的塑性激活区。整体上,300、600和900K的温度下应变分别达到17%、13%和8%时,体系内部FCC结构原子占比开始降低,300K下这种变化是突然发生的,但温度越高,变化发生的越平缓。此外,无论此时体系温度高低,FCC结构原子占比最多,BCC与HCP结构原子占比较少。当应变继续增加,进入应力释放阶段后,在此阶段3种晶体结构的占比随着应变增加而趋于稳定。由此可见,原子级微观尺度下原子排布的变化直接影响着材料的应力-应变关系,这是因为FCC结构原子占比减小会导致体系内部出现HCP与BCC结构,因此,引起位错、层错、滑移等结构出现。此外,温度越高,原子运动更活跃,从而降低了原子间结合力,更容易诱发体系内部原子排序紊乱,更早地诱发不同类型位错的形核,最终体现在弹性模量与应力-应变曲线形貌的差别上。经过以上分析可知,FCC结构原子的演化会诱发晶体学缺陷,因此,在分析材料单轴拉伸形变机制时应将完美的FCC结构原子去除。借助位错提取算法(DislocationExtractionAlgorithm,DXA)对体系内的位错类型及分布进行分析,将分析结果与去除FCC结构原子的体系相结合,以分析GH4169镍基高温合金的形变机制。图4为3种温度下不同应变时的原子排列结构及位错结构特征,其中,片层状原子为HCP结构,零星分布状的单个原子为BCC结构,弥散团簇状与无序状原子为无序结构。同样,以深浅不一的实线表征不同类型的位错。

从图4中可以看出,位错的形核与运动使得体系内部原子结构重排,引发明显的HCP结构层错。层错与层错之间往往以一系列无序排列的原子为界。对于具有FCC结构的GH4169镍基高温合金而言,内部存在的堆垛层错可以等同于HCP结构,宏观下结构的演变表现为塑性形变。随着应变的增加,层错由塑性阶段时体系两端的多形核逐步向体系中间运动,这证明此时会发生颈缩现象。位错大多出现于层错周围,这是因为在外力的作用下,体系内部异常排列的原子极易诱发位错形核,从而降低材料的力学性能。随着应变增加,位错的运动引导层错与层错之间的相互融合趋于稳定,形成沿某个45°方向贯穿整个体系的层错,即形成滑移。此外,位错运动会使异常排序的原子逐步演变成FCC结构,并且吸引异常排序的原子团簇聚集于融合后的层错周围,宏观表现为塑性形变。需要注意的是,在形变过程中体系内会出现由无序原子包裹的空位缺陷,这些空位可以被位错吸收,从而牵引位错与层错运动,这与体系内部不同结构原子占比的变化相一致。另一方面,高温下原子的剧烈运动会导致异常排序的原子增多,为位错形核提供了有利条件的同时增加了体系内部空位的数量。这是因为对于晶体材料而言,空位的形成会受到温度的影响,温度越高,空位形成的概率越大,在此情况下,位错及层错更容易发生运动,与之对应的是材料力学性能的下降。

2.3　形变过程中位错演化

图5仅体现了体系内部位错的类型及特征,以清楚地分析形变过程中位错的特征及演化。图5a、图5d与图5g分别为300、600与920K温度下原子结构体系进入塑性阶段时的位错形貌、类型及分布。从图5中可以看出,材料进入塑性阶段时,位错主要以1/6<112>Shockley不全位错为主,与此同时存在1/2<110>Perfect全位错、1/6<110>Stair-rod压杆位错、1/3<111>Frank分位错、1/3<100>Hirth分位错及其他位错,不同类型的位错具有不同的柏氏矢量,并且1/3<111>Frank分位错及1/3<100>Hirth分位错的含量较小。从图5a、图5d与图5g可以看出,材料刚进入塑性阶段时内部位错长度小、数量多,并且呈现点发射特征,这是因为1/6<112>Shockley不全位错是从空位表面发射,并且随着应变的增加,位错相互结合从而形成位错环,此时部分1/6<112>Shockley不全位错在滑移面上以锐角相交时会形成1/6<110>Stair-rod压杆位错,而以钝角相交时则会形成1/3<100>Hirth分位错。

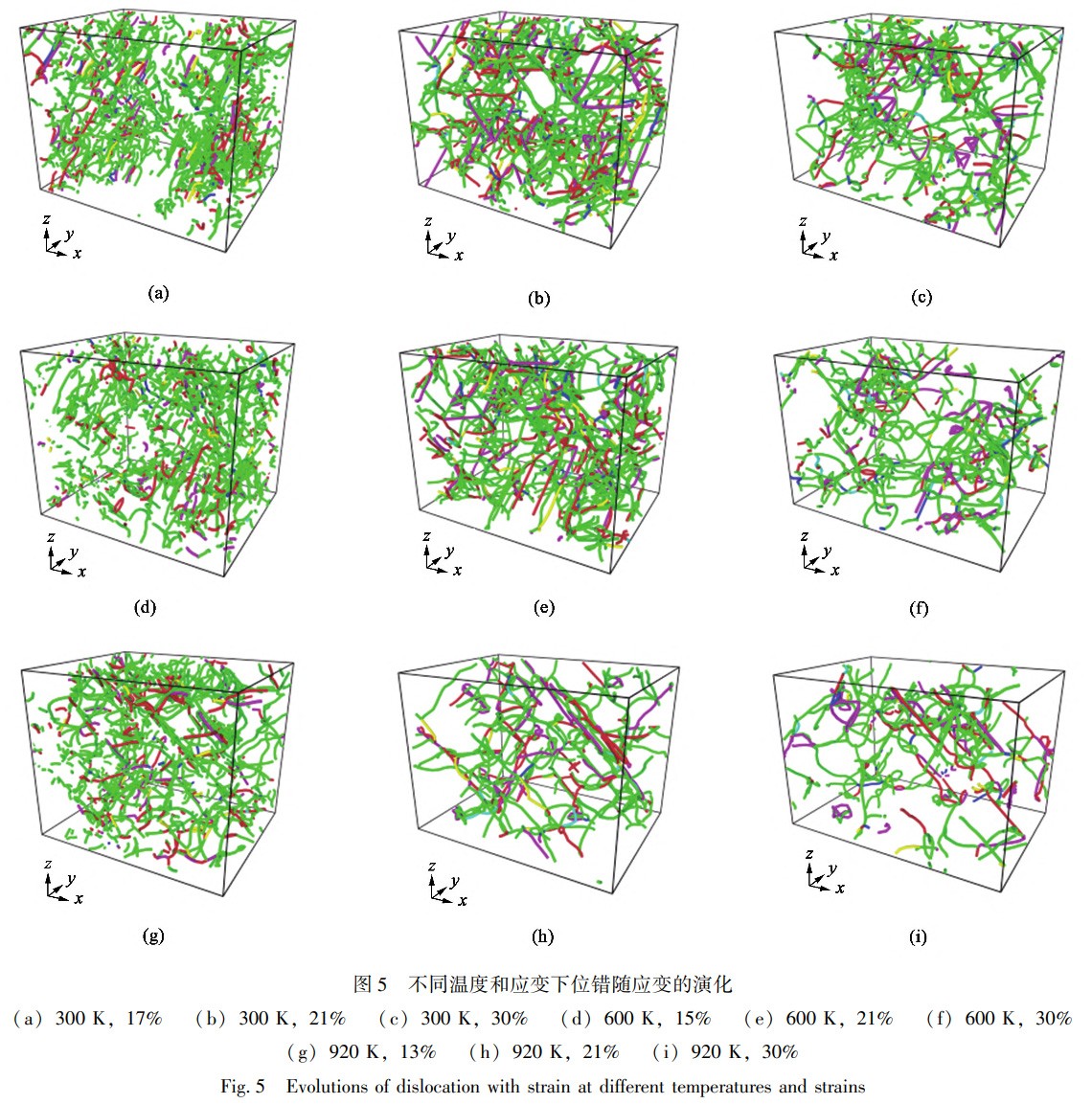
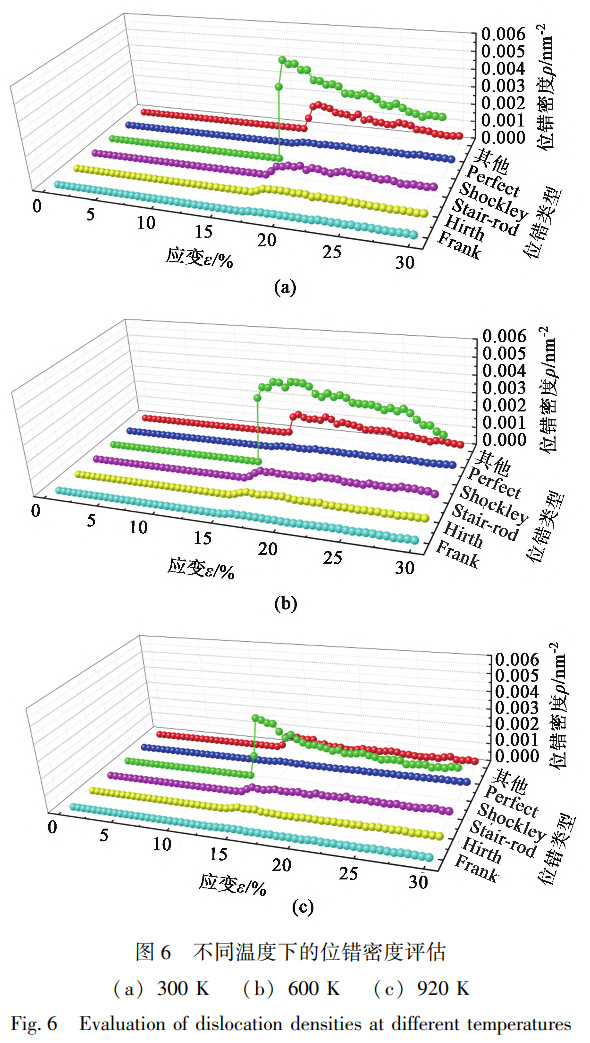
Shockley不全位错通常以刃形位错形式出现,也可以是螺位错或混合型位错,在外力作用下可以在{111}滑移面上运动,从而牵引层错区扩大或缩小,当两个层错区之间夹带了一个定位错时,会形成一个Stair-rod压杆位错,如图5b、图5e与图5h所示。此外,还可以观察到3种温度下均会形成由多个Stair-rod压杆位错包围形成的位错环,结合图4可知,所围区域为层错区域。由于Stair-rod压杆位错属于不可动位错,因此,一定程度上可以在塑性变形阶段使材料发生硬化。应变逐渐增大的同时位错也在不断演化,在此过程中新的Stair-rod压杆位错会形成,并且部分Stair-rod压杆位错会发生解体与扩散,演化为两个可以进行塑性形变的跟踪位错,即Shockley不全位错,如图5c、图5f与图5i所示。在整个拉伸形变过程中,体系内部发生位错形核的同时也会出现空位,空位会引导位错运动,位错运动又会形成新的空位,如此反复,材料内部的层错发生移动和扩展,最终导致滑移。对比不同温度下的位错演化过程可知,温度越高,位错形核位置越均匀,这是因为高温环境下体系内部异常排布的原子的数量多,增大了位错形核的概率。此外,温度越高,位错排布方向的一致性更高,且位错长度更长,这是位错之间更加频繁的相互作用导致的。对不同温度和应变时的位错密度进行评估,结果如图6所示。位错密度[12]计算公式如下:

式中:ρ为位错密度;ldis为体系中位错总长度;V为原子结构体积。从图6可以看出,3种温度下的总位错密度与应力-应变曲线具有一致的变化规律。弹性范围内,随着应变的增加,体系内部各类位错的数量均为0,当材料进入塑性阶段时,Shockley不全位错急剧增加,300、600与920K条件下Shockley不全位错密度的峰值分别为0.0057、0.0048与0.0033nm-2,位错密度的急剧升高证明了材料内部出现了大量层错。随后进入应力释放阶段,在此过程中Shockley位错密度持续降低,而其他类型的位错密度则有所升高,这是因为形变过程中Shockley位错之间不同的相互作用形式使其演化为其他类型位错。此时Stair-rod压杆位错密度在相对稳定的范围内波动,分别为0.0006、0.0005与0.0004nm-2,Stair-rod压杆位错密度的相对稳定证明了材料具有一定的抗变形能力。而造成这种波动的原因是结构为了可以在外力的作用下持续发生变形,迫使Stair-rod压杆位错分解,与此同时又有新的Stair-rod压杆位错形成。总体而言,相对较高的位错密度水平表明,形变过程中材料内部位错反应频繁,并且滑移也较为活跃,尤其是在高温环境下,位错的相互反应更容易发生。

3、结论

(1)室温(300K)、高温(600和920K)的环境下,GH4169镍基高温合金的微观弹性模量分别为125.9、125.3和119.1GPa,且弹性变形范围内的应力-应变曲线形貌差别不大,证明了GH4169镍基高温合金具有良好的高温(920K)抗性。

(2)300、600和900K的温度下应变分别达到17%、13%及8%时体系内部FCC结构原子占比开始降低,温度越高,FCC结构数量降低至最小值时的速率越低。依据体系内部原子结构的演化可将整体形变过程分为弹性区、塑性激活区及应力释放区。

(3)进入塑性激活区后,大量Shockley不全位错形成,并且在随后的形变过程中,Shockley不全位错密度逐渐降低,演化为其他类型位错。进入应力释放区后,各类位错密度保持恒定,滑移的增多及运动使材料出现了颈缩现象。

参考文献:

[1]Plimpton S. Fast parallel algorithms for short-range molecular dynamics [J]. Journal of Computational Physics, 1995, 117: 1-19.

[2]Thompson A P, Aktulga H M, Berger R, et al. LAMMP—A flexiblesimulation tool for particle-based materials modeling at the atomic, meso, and continuum scales [ J ]. Computer Physics Communications, 2022, 271: 10817.

[3]Chen B, Wu W P, Chen M X, et al. Molecular dynamics study of fatigue mechanical properties and microstructural evolution of Nibasedsingle crystal superalloys under cyclic loading [J]. ComputationalMaterials Science, 2020, 185: 109954. [4] 　 Li N L, Wu W P, Nie K. Molecular dynamics study on the evolutionof interfacial dislocation network and mechanical properties of Ni-based single crystal superalloys [J]. Physics Letters A, 2018, 382: 1361-1367.

[5]Li X T, Peng S Y, Zhang X, et al. Microscopic and macroscopic analyses of the interaction mechanism between defect growth and dislocationemission in single-crystal aluminum [J]. Fatigue & Fractureof Engineering Materials & Structures, 2021, 44: 3008-3022.

[6]祝占伟. 镍基合金中五重孪晶形成及变形机理的分子动力学研究 [D]. 大连: 大连理工大学, 2018. Zhun Z W. Study on the Formation and Deformation Mechanisms of Fivefold Twins in Nickel Base Alloy [D]. Dalian: Dalian Universityof Technology, 2018.

[7]Frakas D, Caro A. Model interatomic potentials for Fe-Ni-Cr-CoAlhigh-entropy alloys [J]. Journal of Materials Research, 2020, 35: 3031-3040.

[8]Nandy J, Yedla N, Gupta P, et al. Sintering of AlSi10Mg particlesin direct metal laser sintering process: A molecular dynamics simulation study [ J]. Materials Chemistry and Physics, 2019, 236: 121803.

[9]Wang J Q, Shin S, Hu A M, et al. Diffusion kinetics of transient liquid phase bonding of Ni-based superalloy with Ni nanoparticles: A molecular dynamics perspective [ J]. Computational Materials Science, 2018, 152: 228-235.

[10]Wu W P, Yao Z Z. Molecular dynamics simulation of stress distributionand microstructure evolution ahead of a growing crack in singlecrystal nickel [J]. Theoretical and Applied Fracture Mechanics,2012, 62: 67-75.

[11]杨攀峰. Ni-Co 合金拉伸力学性能和变形机制的模拟研究[D]. 兰州: 兰州理工大学, 2020.

Yang P F. The Simulation Research of Tensile Mechanical Propertiesand Deformation Mechanism of Ni-Co Alloys [D]. Lanzhou: Lanzhou University of Technology, 2020.

[12] Li L, Shen L M, Proust G. Fatigue crack initiation life prediction for aluminium alloy 7075 using crystal plasticity finite element simulations [J]. Mechanics of Materials, 2015, 81: 84-93.

相关链接